삼분탐색..!!(Ternary search)

보통 이분탐색(binary search)에 대해서는 기본적으로 알고있는 경우가 대부분이다. 

하지만 삼분탐색(ternary search)라면 어떨까?!

이분탐색은 정렬되어 있는 수열 속에서 원하는 값을 찾을 때 사용 할 수 있는 탐색 기법이다.

즉, 단조 증가 또는 단조 감소 수열에서 내가 원하는 값이 있는지 없는지를 판단하는 경우에 쓰인다.

삼분탐색은 조금 다른데 오목하거나 볼록한 수열에서 극값을 찾는 탐색이다. 하지만 오목 볼록이 여러번 반복되거나

평평한 (같은 값이 반복되는) 수열에서는 값을 찾을 수 없다. 예를들어, 그래프를 그렸을 때 밑에 그림처럼 나오는 수열에 적용 가능하다.

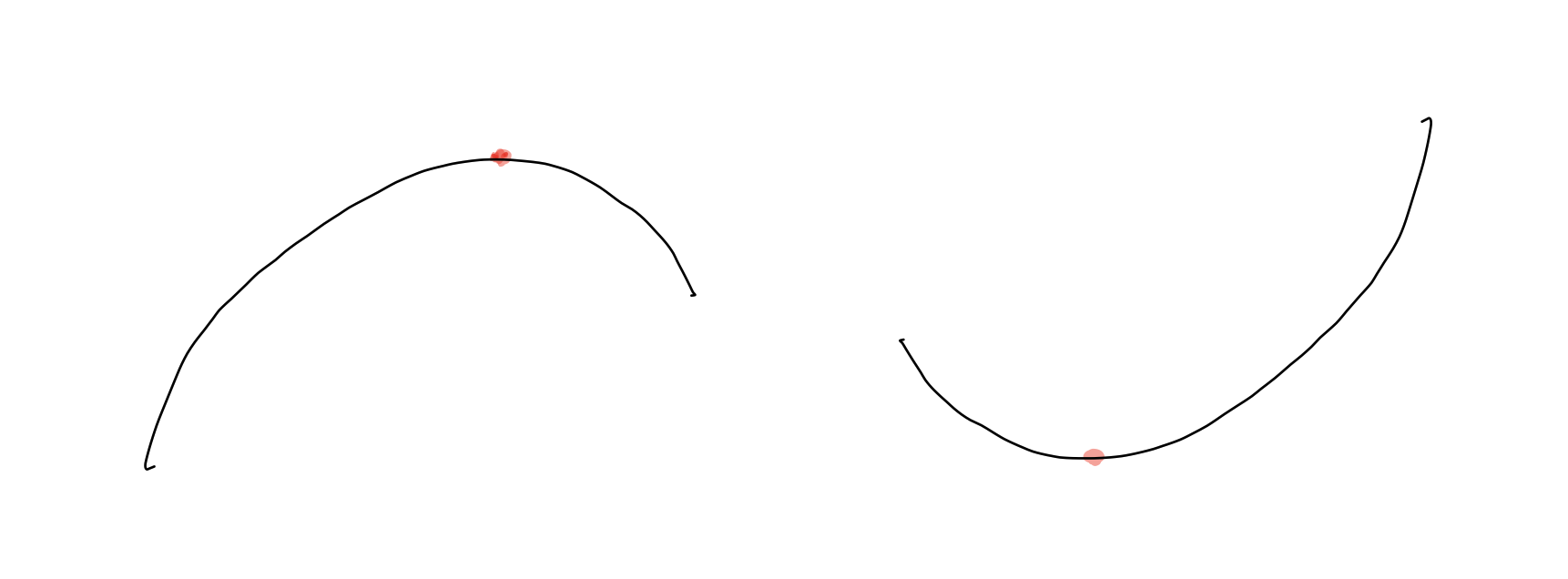
정석적인 삼분탐색의 방법은 극대값을 찾는다 했을 때, 양쪽끝을 기준으로 1/3지점과 2/3지점을 비교하여 둘 중 더 작거나 

같은 쪽의 바깥쪽을 제거 해나가면서 탐색하면 된다.

이 그림의 기준에서는 곡선LR을 삼등분하여 (L, p), (p, q), (q, R)

3부분으로 나누었는데, p의 값이 q의 값보다 작으므로 (L, p)

구간을 제거하고 곡선pR을 LR로 놓고 같은 작업을 반복해 나가면

된다. 이렇게 곡선을 줄여나가다가, L과 R의 차이가 3까지 좁혀지면

3개의 값을 모두 비교해서 가장 큰 값을 찾으면 된다.

 

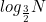
삼분탐색에서 중요한것은 극값을 기준으로 한쪽은 단조 감소, 한쪽은 단조 증가여야 한다는 것이며, 시간복잡도는 

사실 극값을 구하는 건 삼분탐색이 아닌 이분탐색으로도 할 수 있는데 마찬가지로 극대값을 찾는다 했을 때, n보다 n + 1에서의 값이 더 작은

n의 최솟값을 이분탐색으로 찾아내면 된다...!!

백준에 기본적인 삼분탐색으로 푸는 전봇대 문제의 풀이를 올려두었다.

https://mingnine9999.tistory.com/35

백준 8986. 전봇대